housesnax.blogg.se - Travelling salesman problem using dynamic programming in c

In order to iterate through all subsets of '.format(model.objective_value)).

The following figure shows the Dynamic programming subproblems, the recurrence relation and the algorithm for TSP with DP.

It will be convenient to assume that vertices are integers from 1 to n and that the salesman starts his trip in (and also returns back to) vertex 1.

To continue building a cycle, we need to know the last vertex as well as the set of already visited vertices.

A reasonable partial solution in case of TSP is the initial part of a cycle.

A subproblem refers to a partial solution.

Here we shall use dynamic programming to solve TSP: instead of solving one problem we will solve a collection of (overlapping) subproblems.

Some vertices may not be connected by an edge in the general case. Edges weights correspond to the cost (e.g., time) to get from one vertex to another one.

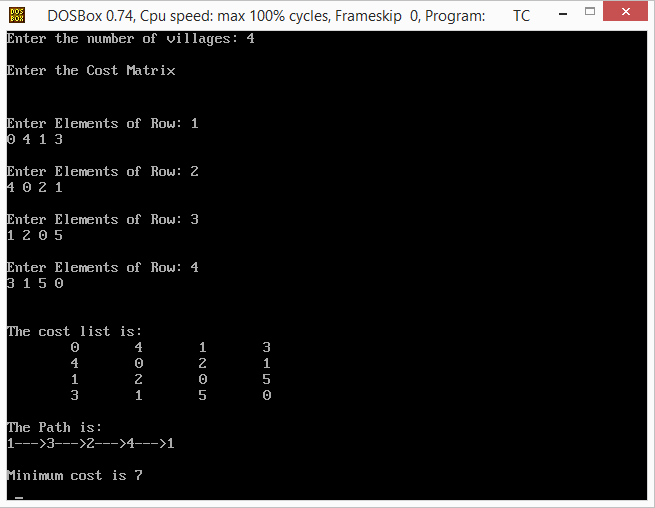
Given a graph with weighted edges, you need to find the shortest cycle visiting each vertex exactly once.

In this problem we shall deal with a classical NP-complete problem called Traveling Salesman Problem. Improving the runtime of the Travelling Salesman Problem with Dynamic Programming Few of the problems discussed here appeared as programming assignments in the Coursera course Advanced Algorithms and Complexity and some of the problem statements are taken from the course. In this blog we shall discuss on the Travelling Salesman Problem (TSP) - a very famous NP-hard problem and will take a few attempts to solve it (either by considering special cases such as Bitonic TSP and solving it efficiently or by using algorithms to improve runtime, e.g., using Dynamic programming, or by using approximation algorithms, e.g., for Metric TSP and heuristics, to obtain not necessarily optimal but good enough solutions, e.g., with Simulated Annealing and Genetic Algorithms) and work on the corresponding python implementations.